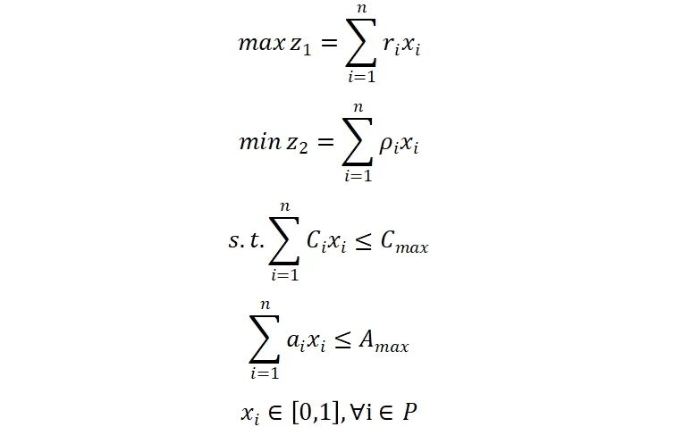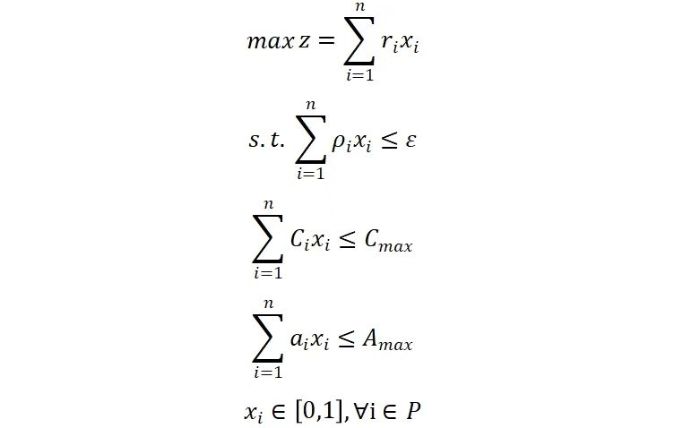中咨视界
刘义成 | 混合整数规划在项目群投资决策中的应用研究
| |||||
| |||||
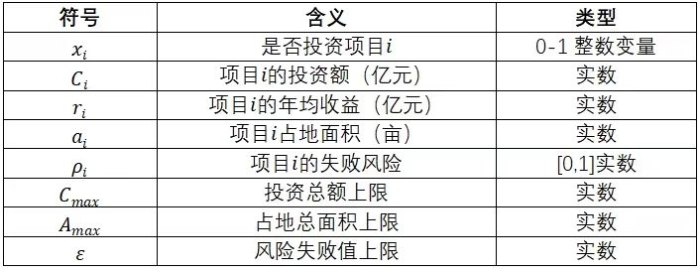
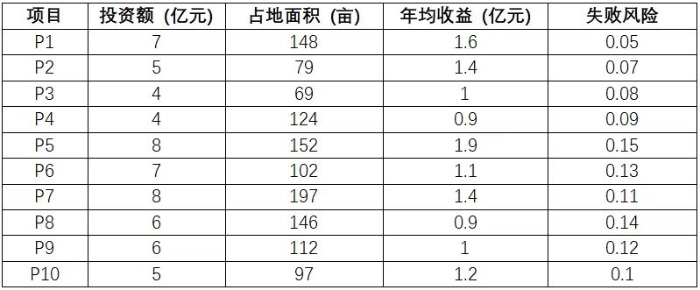
混合整数规划 在项目群投资决策中的应用研究 刘义成 摘要:在高质量发展背景下,为支撑重大战略落地、提升资金使用效益等,政府和企业通常会面临多项目组合优化的投资决策问题。本文以多目标混合整数规划为建模工具,构建一个以项目年均收益最大化为主要目标、失败风险最小化为次要目标的项目群优化决策模型,通过引入ε-约束法将项目失败风险作为约束条件纳入模型体系,采用分支定界法对模型进行精确求解,并通过Python与CBC工具实现数值模拟。研究结果验证了混合整数规划模型在多目标与复杂资源约束条件下的应用价值,为政府或企业开展项目群投资决策提供了定量化分析借鉴。 关键词:项目群投资;混合整数规划;ε-约束法;分支定界法;优化决策 一、引言 当前,我国经济和社会发展已进入高质量发展阶段,在创新驱动发展、构建现代化产业体系、因地制宜发展新质生产力等重大战略的引导下,政府、企业集团等市场主体的项目投资呈现多元化、集群化、系统化的发展趋势,其中,项目群投资决策优化成为需要关注的热点问题,也是固定资产投资决策管理的难点问题[1]。项目群是由若干具有内在联系、资源共享或协同效应的投资项目组合,在当前高质量发展背景下,无论是政府开展的基础设施投资、产业园区建设,还是大型企业集团开展战略性投资,通常都会面临多项目备选、多目标权衡、资源优化配置的复杂决策环境,如在资金、土地等资源限制下,风险与收益平衡的问题。 传统的多项目投资决策问题,主要依赖专家咨询法、层次分析法、净现值法、多准则决策方法等,例如,M Kandakoglu等[2]研究不同多准则方法及其与数学规划技术联合在项目组合选择中的应用;Hui Sun等[3]以BOT高速公路项目为对象,从财务角度计算了具有真实约束的最优投资组合,这些方法在处理当前创新驱动发展下的基础设施规划、产业集群建设等众多项目备选的复杂场景时会显得较为困难。 二、模型建立 目前,在多目标混合整数规划建模研究方面,主要集中在供应链优化、能源管理等领域,如Teh等人[5]通过构建多目标混合整数线性规划模型,研究棕榈油生物质废弃物转化为高收率生物油涉及的年化总利润和全球变暖潜力权衡问题。Jabarzadeh等[6]通过构建可持续水果闭环供应链网络的多目标混合整数线性模型,同时考虑经济、环境和社会指标,即最小化网络总成本和不同网络活动的二氧化碳排放量,同时最大化对需求的响应度同时纳入模型,并采用加权Tchebycheff方法求解Pareto最优解。资源约束下的项目群多目标选择优化问题,核心是在多重约束条件下,选择哪些备选项目,在最大化投资收益的同时,确保整体风险在可容忍的限制范围内。 (一)假设与参数定义 1.基本假设 (1)项目均为独立单元,可被投资或不被投资; (2)已知年均收益、投资额、占地面积、失败风险等指标参数; (3)项目失败风险独立,可简单加和为整体风险水平; (4)项目间不考虑互斥或互补效应; (5)投资为单一决策,不考虑动态分期; (6)组合优化为一次求解,不考虑实时反馈机制。 2.参数定义 设项目集合 ,每个项目具有如下属性变量: 表1 项目属性变量表 (二)混合整数规划模型构建 模型目标包括年均收益最大化的主目标和风险失败风险最小化的次目标,数学表达式如下: 三、算法求解 混合整数规划属于NP-Hard类问题,主要有近似(启发式)算法和精确算法两类求解策略。近似(启发式)算法是在问题规模较大或计算资源有限时,能够快速找到接近最优的可行解,例如遗传算法、模拟退火等,例如,张毅等[7]针对行调冲突的大型高铁站到发线运用优化问题,构建到发线运用多目标优化模型,设计改进遗传算法进行求解。精确算法即能够找到全局最优解,例如分支定界法、分支切割法。本研究选择使用精确算法,即分支定界法,求得真正意义上的最优投资组合。 1.ε约束法 ε约束法由Haimes等人在1971年提出,是一种经典的多目标优化策略,适用于目标函数可解耦的情况,核心思想是保留一个目标函数作为主目标,其余目标函数转化为约束形式,并设置“ε”作为可接受上限或下限。例如,文献[8-10]分别研究了基于模型的ε-约束法在车辆服务设施选址、考虑跑道复杂依赖关系的多目标飞机排序、震后初期多品种应急物资动态分配等领域的Pareto最优解集。通过引入ε约束法,本文构建的模型可以转化为: 2.分支定界法 分支定界法(Branch and Bound)是一种系统性搜索算法,适用于解决混合整数规划问题,例如,Luo Jianchao等[11]针对由放置定时Petri网建模的易死锁柔性制造系统的调度问题,基于网模型的分支树和高度允许的死锁控制器,提出了一种随时分支和约束(AB&B)算法,以最大限度地减少系统工期。利用分支定界法,求解的主要步骤包括:对原问题进行松弛求解获得参考解,即忽略整数约束;若参考解为整数,则为可行解;若参考解非整数,则选择一个非整数变量进行“0-1”分支;对两个子问题分别继续递归求解,并通过求上下界进行定界,以判断是否继续分支或剪枝。该方法保证在有限时间内搜索完所有可能组合,并返回全局最优解。 在本文构建的模型中,每个项目是否选择由决策变量 四、算例分析 为检验上述模型建立和算法求解的有效性,运用PuLP调用内置分支定界法的CBC求解器,进行模拟计算。 1.算例构造 算例中的单个项目参数设置:投资强度,即项目投资额/占地面积,为300—800万元之间的任意值;项目占地面积为30-200亩之间的任意值;年均收益/投资额为0.1-0.3之间的任意值;失败风险为0.1-0.5之间的任意值。算例约束条件为:总投资额不超过30亿元,占地面积不超过500亩。依照项目参数设置,随机生成10个项目的算例参数值如下表: 表2 算例参数值 2.算例求解 基于模型建立和算法求解的思路,使用Python编程语言构建求解流程。核心代码结构包括:载入项目数据,构造参数字典;对每个ε值设定0.2-0.5之间不同的失败风险值;对每个ε值构建并求解一个混合整数规划问题;输出所选项目组合、投资总额、总收益失败风险与占地面积。结果如下表: 表3 算例解集 五、结论 混合整数规划方法在项目群投资决策问题中具有显著优势,其能够有效处理多目标冲突和多资源约束条件下的项目组合优化问题。通过引入ε-约束法,可以平衡项目收益和风险相冲突问题,而采用分支定界法则能显著提升大规模项目组合优化问题的求解效率。该方法在当前政府预算内投资决策、企业战略性投资规划等复杂场景中具有良好的适用性。 参考文献 [1]钱唯克,陈启昉,童林白.基于投资导向决策的项目群优选[J].经营与管理,2019,(09):40-43. [2]M. K ,G. W ,S. B.The use of multi-criteria decision-making methods in project portfolio selection: a literature review and future research directions[J].Annals of Operations Research,2023,332 807-830. [3]Sun H ,Liang Y ,Wang Y , et al.An Optimal Investment Portfolio for BOT Freeway Projects from the Perspective of Transportation and Construction Enterprises[J].KSCE Journal of Civil Engineering,2021,25 1-14. [4]Xu R ,Li S ,Wu J.Multi-Trip Vehicle Routing Problem with Time Windows and Resource Synchronization on Heterogeneous Facilities[J].Systems,2023,11 412-. [5]Chyi K T ,Jully T ,Leng M I C.Multiple Biogenic Waste Valorization via Pyrolysis Technologies in Palm Oil Industry: Economic and Environmental Multi-objective Optimization for Sustainable Energy System[J].Process Integration and Optimization for Sustainability,2023,7 847-860. [6]Jabarzadeh Y ,Yamchi R H ,Kumar V , et al.A multi-objective mixed-integer linear model for sustainable fruit closed-loop supply chain network[J].Management of Environmental Quality An International Journal,2020,ahead-of-print 1351-1373. [7]张毅,李季涛,孙婉婷,等.考虑行调冲突的大型高铁站到发线运用优化研究[J].铁道运输与经济,2025,47 (03):111-121. [8]陈可嘉,司徒腾宽,林鸿熙.考虑跑道复杂依赖关系的多目标飞机排序模型[J].南京航空航天大学学报,2023,55(06):1025-1032. [9]李晓萍,卢葛锋,胡青蜜.震后初期多品种应急物资动态分配模型研究[J].江苏科技大学学报(自然科学版),2023,37 (05):79-86. [10]吴鹏,艾俊.时变需求下多周期车辆服务设施选址多目标优化[J].工业工程与管理,2023,28 (06):164-173. [11] Jianchao L ,Mengchu Z ,Qiang J W.AB&B: An Anytime Branch and Bound Algorithm for Scheduling of Deadlock-Prone Flexible Manufacturing Systems[J].IEEE TRANSACTIONS ON AUTOMATION SCIENCE AND ENGINEERING,2021,18 2011-2021. | |||||
相关链接
- 中国国际工程咨询有限公司系统开发...2025-05-09
- 中咨公司受邀参加国际项目管理协会...2024-10-10
- 中国国际工程咨询有限公司数字化建...2024-01-04
- 中咨(北京)项目管理发展有限公司2023-02-09
- 气脉贯通跨神州 温暖送到千万家:...2022-12-28